In this tutorial, you will learn how to develop a binary classification model to differentiate Red Wine from White Wine using distinct data sets for both the wine types.
Firstly, both the data sets will be combined into a single data set containing both the wine types and an exploratory data analysis will be performed to detect the patterns in the data set.
Secondly, binary classification models will be developed via hyperparameter tuning for Support Vector Machine, Random Forest, and Gradient Boosting classifiers with the help of full feature set.
Finally, important features will be selected from the full feature set based on the correlation with the wine type, and the performance of these stripped-down binary classification models will be compared with the full-fledged classification models.
This tutorial will feature following tools/libraries to classify Wine types using 3 machine learning algorithms namely Support Vector Machine (SVM), Random Forest (RF) and Gradient Boost classifiers:
- Python
- Jupyter Notebook
- scikit-learn
- pandas
- seaborn
- matplotlib
Let’s first make sense of the Wine data itself…
Article Contents
Wine Dataset
Wine data comprises of two datasets for distinct wine types i.e., Red and White. Both the datasets contain numeric features of the relevant wine type. To make a binary classification problem statement, we will combine both the datasets with an extra column indicating the wine type.
Both the datasets are readily available at UCI Machine learning repository, and contains 12 input attributes for each instance. Red Wine contains 1599 instances, where White Wine consists of 4898 instances. We will use these continuous attributes to develop a binary classification model for Red and White wine.
Wine Dataset Link: https://archive.ics.uci.edu/ml/datasets/wine+quality
Input Features
All the input features of the wine dataset are numeric in nature:
- Fixed Acidity
- Volatile Acidity
- Citric Acid
- Residual Sugar
- Chlorides
- Free Sulfur Dioxide
- Total Sulfur Dioxide
- Density
- pH
- Sulphates
- Alcohol
- Quality
Output Features
class: ‘Red’ [for red wine] or ‘white’ [for white wine]
Article Notebook
Code: Red and White Wine binary classification using Support Vector Machines, Random Forest, Gradient Boost
Dataset Link: https://archive.ics.uci.edu/ml/datasets/wine+quality
Prepared By: Awais Naeem (awais.naeem@embedded-robotics.com)
Copyrights: www.embedded-robotics.com
Disclaimer: This code can be distributed with the proper mention of the owner copyrights
Notebook Link: https://github.com/embedded-robotics/datascience/blob/master/wine_dataset_binaryclass_ml/SVM_GB_RF_wine.ipynb
Data Reading and Exploratory Analysis
Let’s first import all python-based libraries necessary to read the data, process it, and then perform further exploratory analysis on it:
import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from sklearn.model_selection import StratifiedKFold, GridSearchCV
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
Now, read both of the data sets in two different pandas data frames. Values are separated by a semi-colon ‘;’, so you will need to specify it as a delimiter to read the correctly formatted columns/values:
red_wine_data = pd.read_csv('winequality-red.csv', delimiter=';')
white_wine_data = pd.read_csv('winequality-white.csv', delimiter=';')
Once you have read the data, it’s a good practice to take a first look at some of the starting rows of the data:
red_wine_data.head()
Output:
fixed acidity volatile acidity citric acid residual sugar chlorides \
0 7.4 0.70 0.00 1.9 0.076
1 7.8 0.88 0.00 2.6 0.098
2 7.8 0.76 0.04 2.3 0.092
3 11.2 0.28 0.56 1.9 0.075
4 7.4 0.70 0.00 1.9 0.076
free sulfur dioxide total sulfur dioxide density pH sulphates \
0 11.0 34.0 0.9978 3.51 0.56
1 25.0 67.0 0.9968 3.20 0.68
2 15.0 54.0 0.9970 3.26 0.65
3 17.0 60.0 0.9980 3.16 0.58
4 11.0 34.0 0.9978 3.51 0.56
alcohol quality
0 9.4 5
1 9.8 5
2 9.8 5
3 9.8 6
4 9.4 5
white_wine_data.head()
fixed acidity volatile acidity citric acid residual sugar chlorides \
0 7.0 0.27 0.36 20.7 0.045
1 6.3 0.30 0.34 1.6 0.049
2 8.1 0.28 0.40 6.9 0.050
3 7.2 0.23 0.32 8.5 0.058
4 7.2 0.23 0.32 8.5 0.058
free sulfur dioxide total sulfur dioxide density pH sulphates \
0 45.0 170.0 1.0010 3.00 0.45
1 14.0 132.0 0.9940 3.30 0.49
2 30.0 97.0 0.9951 3.26 0.44
3 47.0 186.0 0.9956 3.19 0.40
4 47.0 186.0 0.9956 3.19 0.40
alcohol quality
0 8.8 6
1 9.5 6
2 10.1 6
3 9.9 6
4 9.9 6
Add an extra column named ‘class’ in both the datasets to specify the wine type and combine both the datasets in a vertical fashion using pd.concat():
red_wine_data['class'] = 'red'
white_wine_data['class'] = 'white'
wine_data = pd.concat([red_wine_data, white_wine_data], axis=0, ignore_index=True)
Here, you need to set ignore_index=True to get a unique set of index values after combining both the data sets.
Since, you have got the combined data set containing the instances of both the wine types, first thing you need to do is to look for any missing values and deal with them like pros:
wine_data.isnull().sum()
Output:
fixed acidity 0
volatile acidity 0
citric acid 0
residual sugar 0
chlorides 0
free sulfur dioxide 0
total sulfur dioxide 0
density 0
pH 0
sulphates 0
alcohol 0
quality 0
class 0
dtype: int64
Well… Well… Lucky us! No missing values.
Let’s now evaluate the datatypes of each feature to make sure they are ‘numeric’:
wine_data.dtypes
Output:
fixed acidity float64
volatile acidity float64
citric acid float64
residual sugar float64
chlorides float64
free sulfur dioxide float64
total sulfur dioxide float64
density float64
pH float64
sulphates float64
alcohol float64
quality int64
class object
dtype: object
The ‘class’ feature contains ‘white’ or ‘red’, and is therefore classified as ‘object’ type. Let’s convert our ‘class’ feature into a numeric one so that our algorithms can understand the underlying types as well:
wine_data['target'] = np.where(wine_data['class']=='white', 1, 0)
Find the ‘input’ features which form the best correlation with the ‘output’ variable:
wine_data.corr()['target'].sort_values(ascending=True)
Output:
volatile acidity -0.653036
chlorides -0.512678
sulphates -0.487218
fixed acidity -0.486740
density -0.390645
pH -0.329129
alcohol 0.032970
quality 0.119323
citric acid 0.187397
residual sugar 0.348821
free sulfur dioxide 0.471644
total sulfur dioxide 0.700357
target 1.000000
Name: target, dtype: float64
It seems like ‘volatile acidity’, ‘chlorides’, ‘sulphates’ and ‘fixed acidity’ form the negative correlation, whereas ‘free sulfur dioxide’ and ‘total sulfur dioxide’ form the best positive correlation with the ‘target’ value.
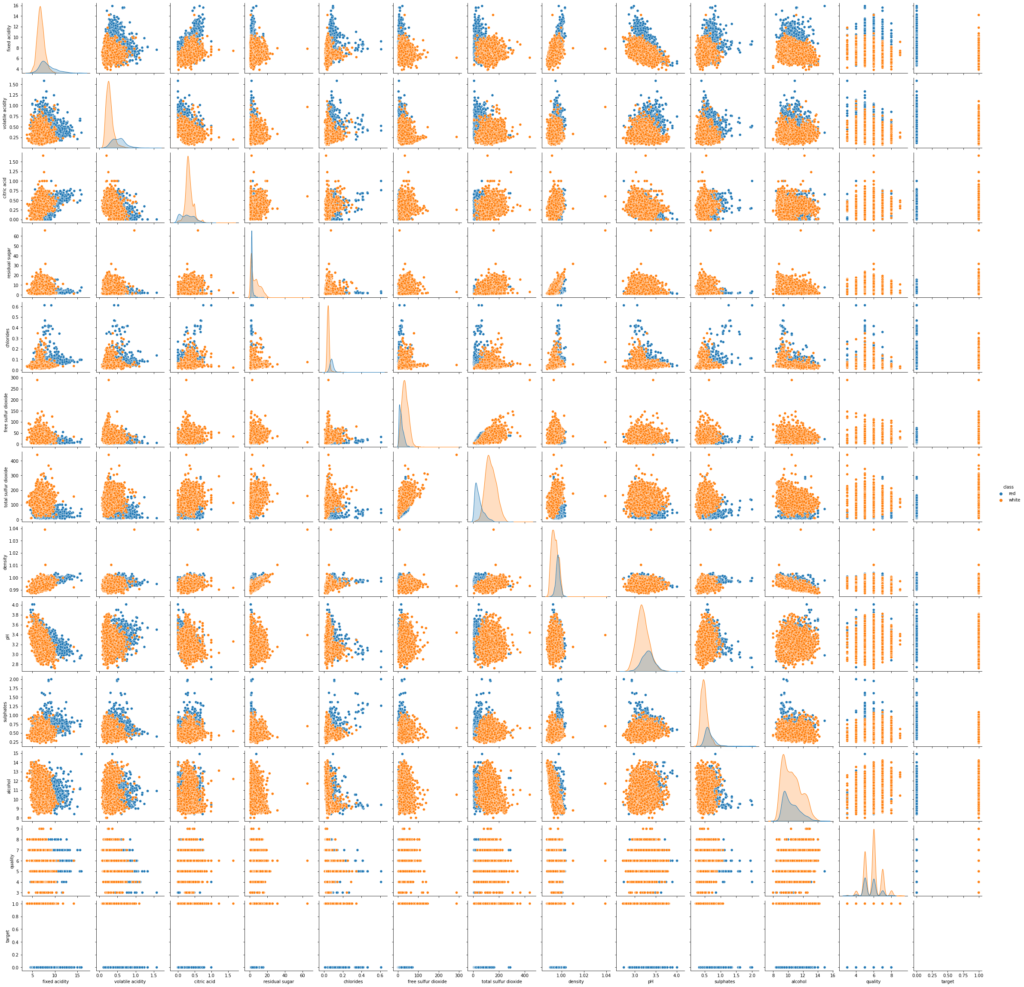
Now draw a pair plot for all the input features and try to spot any more patterns among the data:
sns.pairplot(wine_data, hue='class')
You can also look at the numeric correlation values between each numeric feature using SNS heatmap:
plt.figure(figsize=(15,10))
sns.heatmap(wine_data.corr(), annot=True, vmin=-1, vmax=1, cmap='PiYG')
plt.show()

Here are some salient patterns which I have spotted just by looking at the above two plots:
- Free Sulfur Dioxide and Total Sulfur Dioxide are positively correlated i.e., if you have more of one, you will have more of the other
- Density and Alcohol exhibit a reciprocal relationship i.e., more the concentration of alcohol, less the density
- Density exhibits a positive correlation with the Fixed Acidity and Residual Sugar
- Quality is also positively linked with the amount of Alcohol i.e., more alcohol a wine has, the more its perceived quality. Right, makes sense!
- Volatile Acidity depicts a negative correlation with the Total Sulfur Dioxide
The above relationships are visually plotted as follows:
fig, axes = plt.subplots(2,3, figsize=(18,10))
sns.scatterplot(data=wine_data, x='alcohol', y='density', hue='class', ax=axes[0, 0])
sns.scatterplot(data=wine_data, x='free sulfur dioxide', y='total sulfur dioxide', hue='class', ax=axes[0, 1])
sns.scatterplot(data=wine_data, x='alcohol', y='quality', hue='class', ax=axes[0, 2])
sns.scatterplot(data=wine_data, x='residual sugar', y='density', hue='class', ax=axes[1, 0])
sns.scatterplot(data=wine_data, x='volatile acidity', y='total sulfur dioxide', hue='class', ax=axes[1, 1])
sns.scatterplot(data=wine_data, x='alcohol', y='density', hue='class', ax=axes[1, 2])
plt.show()
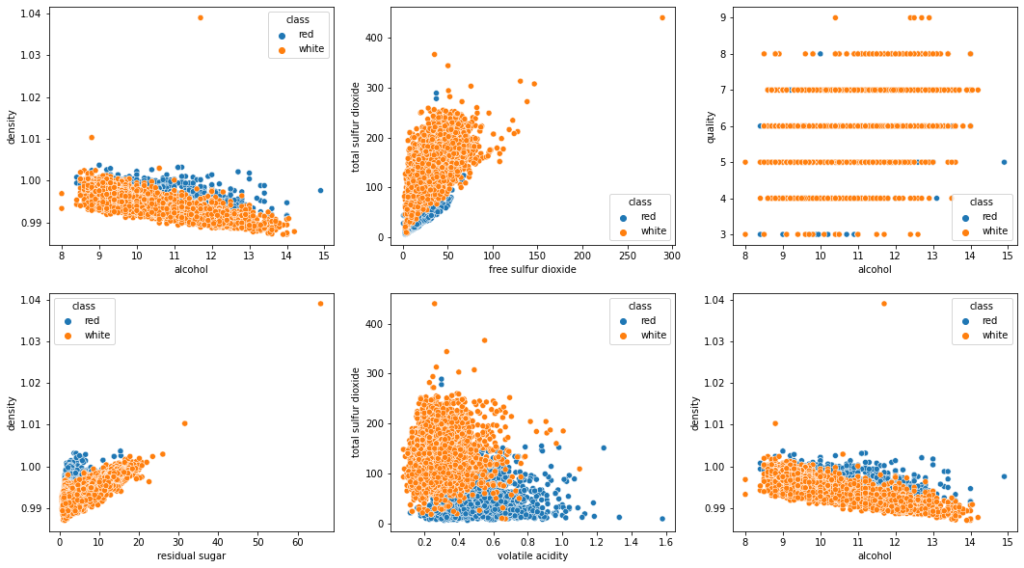
If you can identify more patterns in the data set, do not hesitate to comment and let others know.
Let’s now explore the relation between the input features and the output class. To keep things clean, I will only plot the Kernel Density Estimation of the most important features differentiated by the target class:
fig, axes = plt.subplots(2,3, figsize=(18, 10))
sns.kdeplot(data=wine_data, x='total sulfur dioxide', hue='class', shade='class', ax=axes[0, 0])
sns.kdeplot(data=wine_data, x='free sulfur dioxide', hue='class', shade='class', ax=axes[0, 1])
sns.kdeplot(data=wine_data, x='volatile acidity', hue='class', shade='class', ax=axes[0, 2])
sns.kdeplot(data=wine_data, x='chlorides', hue='class', shade='class', ax=axes[1, 0])
sns.kdeplot(data=wine_data, x='sulphates', hue='class', shade='class', ax=axes[1, 1])
sns.kdeplot(data=wine_data, x='fixed acidity', hue='class', shade='class', ax=axes[1, 2])
plt.show()
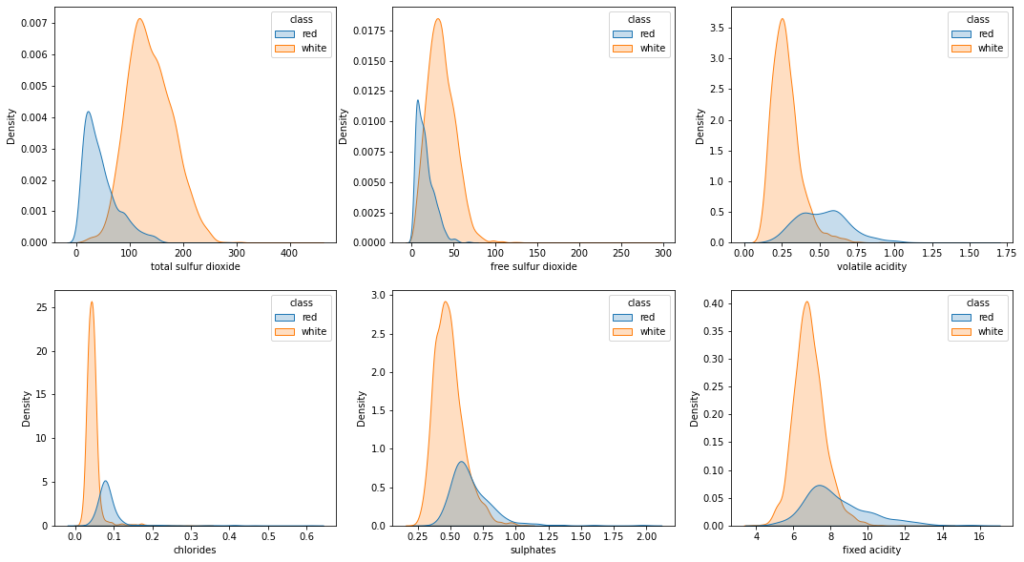
Looking at the KDE plots of these features, following salient points could be noted down:
- All the features are, more or less, normally distributed
- The feature distribution for the ‘Red’ class is right-skewed
- Density of the ‘White’ wine samples is larger than those of ‘Red’ wine which depicts that majority of the wine samples correspond to ‘White’ wine
- Distribution values for Total Sulfur Dioxide, Volatile Acidity, and Chlorides are significantly different for both the wines and can greatly impact the performance of binary classification models
Now let’s do some pre-processing on the data before we can move onto building the binary classification models using machine learning algorithms.
Data Pre-processing
Firstly, drop the ‘class’ feature from the data set as we have already substituted its ‘object’ values into ‘numeric’ ones via ‘target’ feature:
wine_data.drop('class', axis=1, inplace=True)
Specify a uniform datatype for all the features, and separate the Input features of the data from its output class:
wine_data = wine_data.astype('float32')
data_X = wine_data.drop('target', axis=1)
data_y = wine_data['target']
Split the dataset into Training Data (75%) and Testing Data (25%). Training data will be used by the models for training, whereas Testing Data will be used to gauge the performance of the trained models on the unseen data.
X_train, X_test, y_train, y_test = train_test_split(data_X, data_y, test_size=0.25, random_state=1)
Since the input features are numeric and differ in individual scales, they need to be scaled such that the distribution of each feature will have mean=0, and std=1.
StandardScaler() is the industry’s go-to algorithm to perform such scaling, which in-turn, enhances the training capability of the mathematical machine learning models as they need to evaluate each feature having the approx. same distribution.
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
We only need to fit the StandardScaler() on the Training Data and not the Testing Data, since the fitting of scaler on the Testing Data will lead to data leakage.
After the necessary pre-processing, let’s build our first multi-class training model using Support Vector Machine (SVM) and evaluate its performance…
Data Classification using Support Vector Machines
To train the SVM model on the Wine data set, Support Vector Classifier (SVC) is employed from scikit-learn library. At first, SVC() model is fitted on the training data with default parameters:
svm_model = SVC(C=1, kernel='rbf')
svm_model.fit(X_train, y_train)
‘C’ is the regularization parameter which controls underfitting/overfitting. Higher value of ‘C’ leads to less regularization which results in overfitting and vice versa.
‘Kernel’ is selected based on the shape/dimension of the input features. Other values could be ‘linear’, ‘poly’ or ‘sigmoid’.
Once the model is trained, we need to predict the performance of the model on the testing data set:
svm_y_pred = svm_model.predict(X_test)
print('Accuracy Score:', accuracy_score(y_test, svm_y_pred))
print('Confusion Matrix:\n', confusion_matrix(y_test, svm_y_pred))
print('Classification Report:\n', classification_report(y_test, svm_y_pred))
Output:
Accuracy Score 0.9944615384615385
Confusion Matrix
[[ 376 6]
[ 3 1240]]
Classification Report
precision recall f1-score support
0.0 0.99 0.98 0.99 382
1.0 1.00 1.00 1.00 1243
accuracy 0.99 1625
macro avg 0.99 0.99 0.99 1625
weighted avg 0.99 0.99 0.99 1625
So, we have got almost perfect accuracy, recall, and precision scores. Nice, isn’t it?
Let’s now tune hyper-parameters for SVM and evaluate whether we can further enhance the performance of the SVM binary classification model.
Hyperparameter tuning for SVM
In this alternative approach, we will train the model using a subset of hyperparameters and then select best parameters based on a scoring metric i.e., accuracy:
svm_param_grid = {'C':[0.01, 0.1, 1, 10, 100],
'kernel': ['linear', 'rbf'],
'gamma' :[0.001, 0.01, 0.1, 1, 10]}
svm_cv = StratifiedKFold(n_splits=5)
svm_grid = GridSearchCV(SVC(), svm_param_grid, cv=svm_cv, scoring='accuracy')
svm_grid.fit(X_train, y_train)
SVC() model will be trained using each combination of the hyperparameters specified in ‘svm_param_grid’.
During each iteration, model will be trained using 5-fold cross-validation. 4-folds of the data will be used to train the model, and remaining fold will be used to test the accuracy of the trained model.
Also note that we are using ‘StratifiedKFold’ here instead of the legendary ‘Kfold’. The main reason being that White (4898) and Red Wine (1499) samples are not distributed equally in the data set. When making folds during cross validation, ‘StratifiedKFold’ will ensure that fold consists of the same ratio of the white and red wine samples as that of the original dataset.
Hyperparameters resulting in the maximum accuracy will be used to train the model on the complete dataset in the final stages of ‘GridSearchCV’.
We can get the parameters which resulted in the maximum accuracy as follows:
print('SVM best Params:', svm_grid.best_params_)
print('SVM best Score:', svm_grid.best_score_)
Output:
Accuracy Score: 0.9944615384615385
Confusion Matrix:
[[ 376 6]
[ 3 1240]]
Classification Report:
precision recall f1-score support
0.0 0.99 0.98 0.99 382
1.0 1.00 1.00 1.00 1243
accuracy 0.99 1625
macro avg 0.99 0.99 0.99 1625
weighted avg 0.99 0.99 0.99 1625
So, we did improve our accuracy a little bit with the optimized hyperparameters for the support vector machines. With this approach, you will see major differences for dataset having million or more instances.
Let’s now train Random Forest Classifier model on the same data set…
Data Classification using Random Forest Classifier
Random Forest Classifier is basically a lot of decision tree classifiers combining to give the majority vote in favor of a class. You can train a Random Forest classifier using scikit-learn library in Python:
rf_model = RandomForestClassifier(n_estimators=500)
rf_model.fit(X_train, y_train)
‘n_estimators’ specify the number of decision trees which will be used to train the Random Forest classifier.
Let’s observe the accuracy of the Random Forest model on the test data set:
rf_y_pred = rf_model.predict(X_test)
print('Accuracy Score:', accuracy_score(y_test, rf_y_pred))
print('Confusion Matrix:\n', confusion_matrix(y_test, rf_y_pred))
print('Classification Report:\n', classification_report(y_test, rf_y_pred))
Output:
Accuracy Score: 0.992
Confusion Matrix:
[[ 372 10]
[ 3 1240]]
Classification Report:
precision recall f1-score support
0.0 0.99 0.97 0.98 382
1.0 0.99 1.00 0.99 1243
accuracy 0.99 1625
macro avg 0.99 0.99 0.99 1625
weighted avg 0.99 0.99 0.99 1625
Hyperparameter tuning for Random Forest
Similar to what we did for the SVM model, we will tune the hyperparameters of the Random Forest Classifier using 5-fold cross-validation via GridSearchCV() and StratifiedKFold():
rf_param_grid = {'max_samples': [0.1, 0.2, 0.3, 0.4],
'max_features': [5, 6, 7],
'n_estimators' :[50, 100, 500, 1000],
'max_depth': [10, 11, 12]
}
rf_cv = StratifiedKFold(n_splits=5)
rf_grid = GridSearchCV(RandomForestClassifier(), rf_param_grid, cv=rf_cv)
rf_grid.fit(X_train, y_train)
‘max_samples’ denote the fraction of the total samples which all the decision trees will use to specify the individual contribution.
Since there are only 12 input features in the Iris dataset, we will specify a max feature set to be ‘5’, ‘6’ or ‘7’ for more robust model training.
‘max_depth’ denotes the maximum depth of the decision steps for each individual decision tree in the Random Forest model.
After the model is trained, you can get the best model parameters as well as evaluate the performance of the trained model on the test data set:
print('RF best Parameters:', rf_grid.best_estimator_)
print('RF best Score:', rf_grid.best_score_)
Output:
RF best Parameters: RandomForestClassifier(max_depth=10, max_features=5, max_samples=0.4,
n_estimators=500)
RF best Score: 0.9940470699731481
Let’s evaluate the performance of the optimized Random Forest model:
rf_y_pred = rf_grid.predict(X_test)
print('Accuracy:', accuracy_score(y_test, rf_y_pred))
print('Confusion Matrix:\n', confusion_matrix(y_test, rf_y_pred))
print('Classification Report:\n', classification_report(y_test, rf_y_pred))
Output:
Accuray: 0.9907692307692307
Confusion Matrix:
[[ 373 9]
[ 6 1237]]
Classification Report:
precision recall f1-score support
0.0 0.98 0.98 0.98 382
1.0 0.99 1.00 0.99 1243
accuracy 0.99 1625
macro avg 0.99 0.99 0.99 1625
weighted avg 0.99 0.99 0.99 1625
Data Classification using Gradient Boosting Classifier
Gradient Boosting classifier is a combined sequential model of various Decision Trees, where the outcome of one decision tree is used to train the next one and so on.
‘learning_rate’ will specify how much impact outcome of one tree has on the next one. You can control underfitting/overfitting of the gradient boosting classifier using ‘learning_rate’ of the model.
gb_model = GradientBoostingClassifier(n_estimators=500, learning_rate=0.1)
gb_model.fit(X_train, y_train)
‘n_estimators’ specify the number of decision trees to be employed in training the gradient boosting classifier.
gb_y_pred = gb_model.predict(X_test)
print('Accuracy Score:', accuracy_score(y_test, gb_y_pred))
print('Confusion Matrix:\n', confusion_matrix(y_test, gb_y_pred))
print('Classification Report:\n', classification_report(y_test, gb_y_pred))
Output:
Accuracy Score: 0.9926153846153846
Confusion Matrix:
[[ 374 8]
[ 4 1239]]
Classification Report:
precision recall f1-score support
0.0 0.99 0.98 0.98 382
1.0 0.99 1.00 1.00 1243
accuracy 0.99 1625
macro avg 0.99 0.99 0.99 1625
weighted avg 0.99 0.99 0.99 1625
Hyperparameter tuning for Gradient Boosting Classifier
Tuning the hyperparameters for this classifier is more or less similar to that of Random Forest Classifier:
gb_grid_param = {'learning_rate': [0.01, 0.05, 0.1],
'n_estimators' : [10, 50, 100],
'max_depth': [10, 11, 12],
'max_features': [5, 6, 7]}
gb_cv = StratifiedKFold(n_splits=5)
gb_grid = GridSearchCV(GradientBoostingClassifier(), gb_grid_param, cv=gb_cv)
gb_grid.fit(X_train, y_train)
Best parameters and performance of the gradient boosting classifier on the testing set can be evaluated as follows:
print('GB best Parameters:', gb_grid.best_estimator_)
print('GB best Score:', gb_grid.best_score_)
Output:
GB best Parameters: GradientBoostingClassifier(max_depth=10, max_features=5, n_estimators=50)
GB best Score: 0.9963049544569053
gb_y_pred = gb_grid.predict(X_test)
print('Accuray:', accuracy_score(y_test, gb_y_pred))
print('Confusion Matrix:\n', confusion_matrix(y_test, gb_y_pred))
print('Classification Report:\n', classification_report(y_test, gb_y_pred))
Output:
Accuray: 0.9932307692307693
Confusion Matrix:
[[ 373 9]
[ 2 1241]]
Classification Report:
precision recall f1-score support
0.0 0.99 0.98 0.99 382
1.0 0.99 1.00 1.00 1243
accuracy 0.99 1625
macro avg 0.99 0.99 0.99 1625
weighted avg 0.99 0.99 0.99 1625
Important Features of Wine Data
Previously, we have trained our classification models using the full feature set of the wine data set which is acceptable in some cases. However, most of the times, we need to only consider the features which play a significant role in identifying the target values and then train the models using such features.
This has a larger impact of reducing the training time as well as the consumption of computation resources. As we have already entered the regime of Cloud based distributed training platforms, the need for identifying the most relevant features out of the feature set is a critical requirement.
For our dataset, we have already identified the critical features during exploratory data analysis i.e., “total sulfur dioxide”, “volatile acidity”, “chlorides”, “sulphates”, “fixed acidity”, “free sulfur dioxide”.
Let’s now extract a dataset consisting of these features only:
features = ["total sulfur dioxide", "volatile acidity", "chlorides", "sulphates", "fixed acidity", "free sulfur dioxide"]
data_X = wine_data[features]
data_y = wine_data['target']
Split the data into Training (75%) and Testing (25%) instances, and standardize the input ‘numeric’ features:
X_train, X_test, y_train, y_test = train_test_split(data_X, data_y, test_size=0.25, random_state=1)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
Binary Classification using the Important Features
We will now train the machine learning models on this stripped-down data set, and compare their performance with the models trained on the full-fledged feature set.
So, let’s start with the support vector machines (SVM)…
Support Vector Machine (SVM) Training
Specify the features of the SVM model which were obtained after hyper-parameter tuning, and let the model train on the new feature set:
svm_model = SVC(C = 10, gamma = 0.01, kernel='rbf')
svm_model.fit(X_train, y_train)
Now, evaluate the performance of the trained SVM model using the Test instances of the dataset:
svm_y_pred = svm_model.predict(X_test)
print('Accuracy Score:', accuracy_score(y_test, svm_y_pred))
print('Confusion Matrix:\n', confusion_matrix(y_test, svm_y_pred))
print('Classification Report:\n', classification_report(y_test, svm_y_pred))
Output:
Accuracy Score: 0.9815384615384616
Confusion Matrix:
[[ 369 13]
[ 17 1226]]
Classification Report:
precision recall f1-score support
0.0 0.96 0.97 0.96 382
1.0 0.99 0.99 0.99 1243
accuracy 0.98 1625
macro avg 0.97 0.98 0.97 1625
weighted avg 0.98 0.98 0.98 1625
Full-Feature SVM Model Accuracy: 0.994
Important-Features SVM Model Accuracy: 0.982
So, we have got almost similar accuracy with almost half the features.
Interesting, right?
Let’s move on to the next training model i.e, Random Forest Classifier…
Random Forest Classifier Training
Specify the parameters of the Random Forest model obtained after hyperparameter optimization, and train the model on the important features:
rf_model = RandomForestClassifier(max_depth=10, max_features=6, max_samples=0.4, n_estimators=50)
rf_model.fit(X_train, y_train)
Once the model is trained, evaluate its performance on the test dataset as follows:
rf_y_pred = rf_model.predict(X_test)
print('Accuracy Score:', accuracy_score(y_test, rf_y_pred))
print('Confusion Matrix:\n', confusion_matrix(y_test, rf_y_pred))
print('Classification Report:\n', classification_report(y_test, rf_y_pred))
Output:
Accuracy Score: 0.9833846153846154
Confusion Matrix:
[[ 372 10]
[ 17 1226]]
Classification Report:
precision recall f1-score support
0.0 0.96 0.97 0.96 382
1.0 0.99 0.99 0.99 1243
accuracy 0.98 1625
macro avg 0.97 0.98 0.98 1625
weighted avg 0.98 0.98 0.98 1625
Full-Feature Random Forest Model Accuracy: 0.990
Important-Features Random Forest Model Accuracy: 0.983
So, we have got almost similar accuracy. Our magic with the important features seems to be working.
Let’s now train our final model i.e., Gradient Boosting Classifier…
Gradient Boosting Classifier Training
Train the model using the best parameters obtained after hyperparameter optimization, and evaluate the performance of the model on the testing data set:
gb_model = GradientBoostingClassifier(learning_rate=0.001, n_estimators=10, max_depth=10, max_features=5)
gb_model.fit(X_train, y_train)
gb_y_pred = gb_model.predict(X_test)
print('Accuracy Score:', accuracy_score(y_test, gb_y_pred))
print('Confusion Matrix:\n', confusion_matrix(y_test, gb_y_pred))
print('Classification Report:\n', classification_report(y_test, gb_y_pred))
Output:
Accuracy Score: 0.9889230769230769
Confusion Matrix:
[[ 375 7]
[ 11 1232]]
Classification Report:
precision recall f1-score support
0.0 0.97 0.98 0.98 382
1.0 0.99 0.99 0.99 1243
accuracy 0.99 1625
macro avg 0.98 0.99 0.98 1625
weighted avg 0.99 0.99 0.99 1625
Full-Feature Random Forest Model Accuracy: 0.993
Important-Features Random Forest Model Accuracy: 0.988
Gradient Boosting classifier also seems to train the model well even when half the features are stripped off. Nice, isn’t it?
Conclusion
In this tutorial, we developed Support Vector Machine, Random Forest and Gradient Boost classification models for 2-class wine data set. These classification models helped us identify the Red and White wine types using numeric input features. The hyperparameters of all the models were also tuned to optimize the performance of the classification model for all the algorithms.
Moreover, the models were trained using the more correlated features of the data set (6 features) and their performance was almost same when compared with the models developed using the full-fledge feature set (12 features). These results depicted that robust model could be trained using the important features only, which is a critical requirement to save computation resources as well as the training time.
Models were trained on the training data (75%), and their performance was evaluated using testing data (25%). Approx. accuracy of 99% showed that all of the trained models were able to differentiate the Red Wine from the White Wine.

He is the owner and founder of Embedded Robotics and a health based start-up called Nema Loss. He is very enthusiastic and passionate about Business Development, Fitness, and Technology. Read more about his struggles, and how he went from being called a Weak Electrical Engineer to founder of Embedded Robotics.

Subscribe for Latest Articles
Don't miss new updates on your email!