In this tutorial, you will learn how to develop a regression model to estimate the house prices in Boston area using Linear Regression, Support Vector Machine, Random Forest, and Gradient Boosting models.
Regular training approach will use full feature set to estimate the final price of the houses. However, an alternative approach will extract the important features out of the full feature set and train the regression models on the stripped-down feature set.
Moreover, performance of the models trained using both the approaches will be compared in terms of Minimum Absolute Error, Minimum Squared Error, and R2 Score.
This tutorial will feature following tools/libraries to predict the house prices:
- Python
- Jupyter Notebook
- scikit-learn
- pandas
- seaborn
- matplotlib
Let’s first make sense of the Boston Housing Data…
Article Contents
Boston Housing Dataset
Housing dataset comprises of information about housing values in the suburbs of Boston. There are total of 506 instances with each instance specifying 13 continuous attributes (including the output attribute “MEDV”) and 1 binary-valued attribute.
Each instance quantifies a cumulative feature of the Boston suburb and the Median Value (MEDV) of the owner-occupied homes in the suburb. We will use the input attributes of this dataset to train the regression models, and then predict the prices of the houses using the trained models:
The dataset is available at UCI machine learning laboratory, and can be downloaded using the following link: Boston Housing Dataset Link: https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
Input Features
- CRIM: Per capita crime rate by town
- ZN: Proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS: Proportion of non-retail business acres per town
- CHAS: Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX: Nitric Oxides concentration (parts per 10 million)
- RM: average number of rooms per dwelling
- AGE: Proportion of owner-occupied units built prior to 1940
- DIS: Weighted distances to five Boston employment centres
- RAD: Index of accessibility to radial highways
- TAX: Full-value property-tax rate per $10,000
- PTRATIO: Pupil-teacher ratio by town
- B: 1000(Bk – 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT: Percent lower status of the population
Output Features
MEDV: Median value of owner-occupied homes in $1000’s
Article Notebook
Code: Boston Housing Dataset Regression Modelling – Price Estimation using Support Vector Machines, Random Forest, Gradient Boost, and Linear Regression
Dataset Link: https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
Prepared By: Awais Naeem (awais.naeem@embedded-robotics.com)
Copyrights: www.embedded-robotics.com
Disclaimer: This code can be distributed with the proper mention of the owner copyrights
Notebook Link: https://github.com/embedded-robotics/datascience/blob/master/housing_dataset_regression_ml/SVM_GB_RF_LR_housing.ipynb
Data Reading and Exploratory Analysis
Let’s first import all python-based libraries necessary to read the data, process it, and then perform further exploratory analysis on it:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.svm import SVR
%matplotlib inline
As the dataset does not contain any column names, so you will need to specify those while reading the data in a pandas data frame. Also the values are separated by a white-space, so you will need to specify it as a delimiter to read the correctly formatted columns/values:
housing_data_columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'Bk', 'LSTAT', 'MEDV']
housing_data = pd.read_csv('housing.data', header=None, delim_whitespace=True, names=housing_data_columns)
housing_data.head()
Output:
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX \
0 0.00632 18.0 2.31 0 0.538 6.575 65.2 4.0900 1 296.0
1 0.02731 0.0 7.07 0 0.469 6.421 78.9 4.9671 2 242.0
2 0.02729 0.0 7.07 0 0.469 7.185 61.1 4.9671 2 242.0
3 0.03237 0.0 2.18 0 0.458 6.998 45.8 6.0622 3 222.0
4 0.06905 0.0 2.18 0 0.458 7.147 54.2 6.0622 3 222.0
PTRATIO Bk LSTAT MEDV
0 15.3 396.90 4.98 24.0
1 17.8 396.90 9.14 21.6
2 17.8 392.83 4.03 34.7
3 18.7 394.63 2.94 33.4
4 18.7 396.90 5.33 36.2
Once you have read the data into a proper formatted data frame, first thing you need to do is to look for any missing values:
housing_data.isnull().sum()
Output:
CRIM 0
ZN 0
INDUS 0
CHAS 0
NOX 0
RM 0
AGE 0
DIS 0
RAD 0
TAX 0
PTRATIO 0
Bk 0
LSTAT 0
MEDV 0
dtype: int64
So, we have got no missing values. Let’s now evaluate the datatypes of each attribute to make sure they are ‘numeric’:
housing_data.dtypes
Output:
CRIM float64
ZN float64
INDUS float64
CHAS int64
NOX float64
RM float64
AGE float64
DIS float64
RAD int64
TAX float64
PTRATIO float64
Bk float64
LSTAT float64
MEDV float64
dtype: object
Now convert the datatype of each attribute to uniform datatype i.e., ‘float32’:
housing_data = housing_data.astype('float32')
Find the ‘input’ features which form the best correlation with the ‘output’ variable:
data_corr = housing_data.corr()
data_corr['MEDV']
Output:
CRIM -0.388305
ZN 0.360445
INDUS -0.483725
CHAS 0.175260
NOX -0.427321
RM 0.695360
AGE -0.376955
DIS 0.249929
RAD -0.381626
TAX -0.468536
PTRATIO -0.507787
Bk 0.333461
LSTAT -0.737663
MEDV 1.000000
Name: MEDV, dtype: float64
It seems like ‘LSTAT, ‘PTRATIO, ‘TAX’, ‘NOX’ and ‘INDUS’ negatively impact the housing prices, whereas ‘RM’ depicts the positive correlation with the ‘MEDV’ value.
Now draw a pair plot for all the input features and try to spot any more patterns among the data:
sns.pairplot(housing_data)

You can also look at the numeric correlation values between each numeric feature using SNS heatmap:
plt.figure(figsize=(20,10))
sns.heatmap(data_corr, vmin=-1, vmax=1, cmap='PiYG', annot=True)
plt.show()

Looking at the SNS heatmap and the pairplot, we can easily spot the following patterns in the data set:
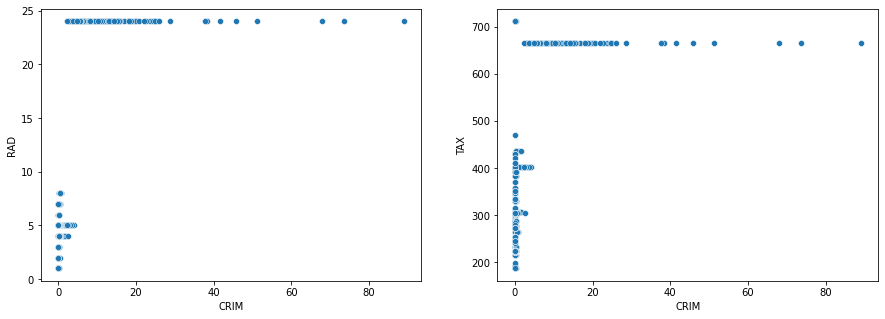
More accessibility to radial highways (RAD) and tax rate (TAX) resulted in more per capita crime rate (CRIM):
fig, axes = plt.subplots(1, 2, sharex = True, figsize=(15, 5))
sns.scatterplot(data=housing_data, x='CRIM', y='RAD', ax=axes[0])
sns.scatterplot(data=housing_data, x='CRIM', y='TAX', ax=axes[1])
plt.show()
More proportion of residential land zones (ZN) resulted in less non-retail business acres (INDUS), Nitric oxides concentration (NOX), and owner-occupied houses (AGE) which is really a cause-and-effect scenario. Moreover, less proportion of residential land resulted in less distances to Boston employment centers:
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
sns.scatterplot(data=housing_data, x='ZN', y='INDUS', ax=axes[0, 0])
sns.scatterplot(data=housing_data, x='ZN', y='NOX', ax=axes[0, 1])
sns.scatterplot(data=housing_data, x='ZN', y='AGE', ax=axes[1, 0])
sns.scatterplot(data=housing_data, x='ZN', y='DIS', ax=axes[1, 1])
plt.show()

More proportion of non-retail business acres (INDUS) had the effect of increasing Nitric Oxide concentration (NOX), owner-occupied houses (AGE), accessibility to radial highways (RAD), tax rate (TAX), and percentage of population having low status (LSTAT). Besides, more non-retail business acres resulted in a decreased distance to major Boston employment centers which is a cause-and-effect scenario as people will seek employments in the nearby businesses:
fig, axes = plt.subplots(2, 3, figsize=(18, 10))
sns.scatterplot(data=housing_data, x='INDUS', y='NOX', ax=axes[0, 0])
sns.scatterplot(data=housing_data, x='INDUS', y='AGE', ax=axes[0, 1])
sns.scatterplot(data=housing_data, x='INDUS', y='DIS', ax=axes[0, 2])
sns.scatterplot(data=housing_data, x='INDUS', y='RAD', ax=axes[1, 0])
sns.scatterplot(data=housing_data, x='INDUS', y='TAX', ax=axes[1, 1])
sns.scatterplot(data=housing_data, x='INDUS', y='LSTAT', ax=axes[1, 2])
plt.show()

More owner-occupied houses (AGE), accessibility to radial highways (RAD), and tax rate (TAX) ultimately resulted in more nitric oxide concentration (NOX) in the area. Also, the increasing distance to Boston employment centers (DIS) seemed to decrease the nitric oxide concentration:
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
sns.scatterplot(data=housing_data, x='NOX', y='AGE', ax=axes[0, 0])
sns.scatterplot(data=housing_data, x='NOX', y='DIS', ax=axes[0, 1])
sns.scatterplot(data=housing_data, x='NOX', y='RAD', ax=axes[1, 0])
sns.scatterplot(data=housing_data, x='NOX', y='TAX', ax=axes[1, 1])
plt.show()

More owner-occupied houses (AGE) resulted in more percentage of low-status population (LSTAT), whereas more LSTAT resulted in averagely smaller number of rooms per dwelling (RM):
fig, axes = plt.subplots(1, 2, sharex = True, figsize=(15, 5))
sns.scatterplot(data=housing_data, x='LSTAT', y='RM', ax=axes[0])
sns.scatterplot(data=housing_data, x='LSTAT', y='AGE', ax=axes[1])
plt.show()

More accessibility to radial highways (RAD) and percentage of low status population had the effect of the imposition of more tax (TAX):
fig, axes = plt.subplots(1, 2, sharex = True, figsize=(15, 5))
sns.scatterplot(data=housing_data, x='TAX', y='RAD', ax=axes[0])
sns.scatterplot(data=housing_data, x='TAX', y='LSTAT', ax=axes[1])
plt.show()

If you can identify more patterns in the data set, do not hesitate to comment and let others know.
Let’s now explore the relation between median price of homes (MEDV) and more correlated attributes in the housing data set:
fig, axes = plt.subplots(2, 3, figsize=(18, 10))
sns.scatterplot(data=housing_data, x='MEDV', y='INDUS', ax=axes[0, 0])
sns.scatterplot(data=housing_data, x='MEDV', y='NOX', ax=axes[0, 1])
sns.scatterplot(data=housing_data, x='MEDV', y='RM', ax=axes[0, 2])
sns.scatterplot(data=housing_data, x='MEDV', y='PTRATIO', ax=axes[1, 0])
sns.scatterplot(data=housing_data, x='MEDV', y='TAX', ax=axes[1, 1])
sns.scatterplot(data=housing_data, x='MEDV', y='LSTAT', ax=axes[1, 2])
plt.show()

Looking at the scatter plots of correlated features against the house prices, following salient points could be noted down:
- More proportion of non-retail business acres (INDUS) results in declining housing prices in the area
- Housing prices decrease with the increasing concentration of nitric dioxide (NOX), and vice versa. This is quite evident as people tend to leave the areas concentrated in high impurity gases.
- More number of rooms per dwelling (RM) result in the augmenting prices of the houses. An interesting finding, right?
- More public-teacher ratio (PTRATIO) has the result of declining house prices
- More tax rate (TAX) has the result of decreasing the price. Well… you cannot do much about the Government-Public issues
- More percentage of low-status population (LSTAT) has the overall effect of reduced house prices in the area. This seems to be the result of human psychology in the context of status quo as people like to associate themselves to expensive things
Now since we are done with the exploratory data analysis and found some useful insights into the housing data, let’s do some pre-processing on the data before we can actually train the algorithms to predict the house prices…
Data Pre-processing
Firstly, differentiate the ‘input features’ from the ‘output feature’:
data_X = housing_data.drop('MEDV', axis=1)
data_y = housing_data['MEDV']
Split the dataset into Training Data (80%) and Testing Data (20%). Training data will be used by the models for training purpose, whereas Testing Data will be used to gauge the performance of the trained models on the unseen data.
X_train, X_test, y_train, y_test = train_test_split(data_X, data_y, test_size=0.2, random_state=0)
Since the input features are numeric and differ in individual scales, they need to be scaled such that the distribution of each feature will have mean=0, and std=1.
StandardScaler() is the industry’s go-to algorithm to perform such scaling, which in-turn, enhances the training capability of the mathematical machine learning models as they need to evaluate each feature having the approx. same distribution.
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
We only need to fit the StandardScaler() on the Training Data and not the Testing Data, since the fitting of scaler on the Testing Data will lead to data leakage.
Important Features of Housing Dataset
After training the models on the full feature set, we will train the models on the selected feature set and compare the performance of both the trained models. This will give us an idea whether we can achieve the comparable performance using a limited number of features.
Using a limited number of features to train a learning model has the advantage of consuming less training time as well as the computation resources.
The correlation of each feature with the target attribute i.e., MEDV will help us select the most important features:
target_corr = data_corr['MEDV']
target_corr
Output:
CRIM -0.388305
ZN 0.360445
INDUS -0.483725
CHAS 0.175260
NOX -0.427321
RM 0.695360
AGE -0.376955
DIS 0.249929
RAD -0.381626
TAX -0.468536
PTRATIO -0.507787
Bk 0.333461
LSTAT -0.737663
MEDV 1.000000
Name: MEDV, dtype: float64
Now, let us select the features having absolute correlation value in excess of 0.4:
imp_features = target_corr.index[abs(target_corr) > 0.4]
imp_features = imp_features[imp_features != 'MEDV']
print(imp_features)
Output:
Index(['INDUS', 'NOX', 'RM', 'TAX', 'PTRATIO', 'LSTAT'], dtype='object')
Differentiate the input attributes from the output attribute, and split the dataset into training/testing data:
data_X_imp = data_X[imp_features]
data_y_imp = data_y
X_train_imp, X_test_imp, y_train_imp, y_test_imp = train_test_split(data_X_imp, data_y_imp, test_size=0.2, random_state=0)
Since we are done with the necessary pre-processing, let’s build our first regression model using Linear/Ridge Regression algorithms and evaluate their performance…
Regression Modelling Performance Parameters
The performance of the regression model can be evaluated in terms of Mean Absolute Error (MAE), Mean Squared Error (MSE) or R-Squared(R2) Score.
Mean Absolute Error represents the mean of absolute error between the original values and the values predicted from the model. So, the lower the MAE, the better.
Mean Squared Error depicts the mean of square of the error between the original values and the predictions from the model. So, we should aim for a lower MSE value.
R-Squared represents the proportion of the variance in the dependent variable that is predictable from the independent variable. So, R2 value must be as close to ‘1’ as possible
Regression Modelling using Linear/Ridge Regression
To train the linear and ridge regression models on the housing dataset, we need to employ these from scikit-learn library. We will firstly train and evaluate the models on the full feature set and then on the important feature set.
Full Feature Set
Linear Regression
To train Linear Regression using the full feature set, select the appropriate training data (X_train, y_train) and fit the model as follows:
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)
Let’s now evaluate the performance of this Linear Regression model:
lr_y_pred = lr_model.predict(X_test)
print('Mean Absolute Error:', mean_absolute_error(y_test, lr_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test, lr_y_pred))
print('R2 Score:', r2_score(y_test, lr_y_pred))
Output:
Mean Absolute Error: 3.8429098
Mean Squared Error: 33.448986
R2 Score: 0.5892223213577091
MAE and MSE represents the value in $1000’s since the output variable units are the same. These values are not bad for a prediction, but can be improved further.
Ridge Regression
Ridge regression is a derivative of linear regression, but with L2 regularization. It reduces the model complexity by shrinking the coefficients as per the square of the magnitude of coefficients.
Since the L2 regularization is controlled by a number of hyperparameters, we will do a GridSearch to select the best suite of hyperparameters and then train our model using those parameters:
ridge_model = Ridge()
ridge_param_grid = {'solver': ['svd', 'cholesky', 'lsqr', 'sag'],
'alpha': [1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 1, 10, 100],
'fit_intercept': [True, False],
'normalize': [True, False]
}
ridge_cv = KFold(n_splits=5)
ridge_grid = GridSearchCV(ridge_model, ridge_param_grid, cv=ridge_cv, scoring='neg_mean_absolute_error', n_jobs=-1)
ridge_grid.fit(X_train, y_train)
Note that we are using ‘neg_mean_absolute_error’ here as the scoring parameter. The reason is that GridSearchCV() tries to maximizes the scoring value during hyperparameter tuning. A higher value of neg_mean_absolute_error will result in low mean_absolute_error which is ultimately our requirement.
print('Ridge Regression Best Params:', ridge_grid.best_params_)
print('Ridge Regression Best Score:', ridge_grid.best_score_)
Output:
Ridge Regression Best Params: {'alpha': 0.1, 'fit_intercept': True, 'normalize': True, 'solver': 'sag'}
Ridge Regression Best Score: -3.1917717933654783
Let’s evaluate the performance of the ridge regression model on the testing data set:
ridge_y_pred = ridge_grid.predict(X_test)
print('Mean Absolute Error:', mean_absolute_error(y_test, ridge_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test, ridge_y_pred))
print('R2 Score:', r2_score(y_test, ridge_y_pred))
Output:
Mean Absolute Error: 3.9140587
Mean Squared Error: 36.11566
R2 Score: 0.5564736415496676
So, we have slightly lower performance of the ridge regression as compared to linear regression. However, given the reduction in the model complexity, these numbers are quite acceptable.
Important Feature Set
Linear Regression
Select the dataset consisting of important feature set (X_train_imp, y_train_imp) and fit the regression model on that data:
lr_model = LinearRegression()
lr_model.fit(X_train_imp, y_train_imp)
Now evaluate its performance on the testing data:
lr_y_pred = lr_model.predict(X_test_imp)
print('Mean Absolute Error:', mean_absolute_error(y_test_imp, lr_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test_imp, lr_y_pred))
print('R2 Score:', r2_score(y_test_imp, lr_y_pred))
Output:
Mean Absolute Error: 4.394505
Mean Squared Error: 42.651993
R2 Score: 0.47620272483367654
Full Feature Set: MAE – 3.84, MSE – 33.44, R2 – 0.59
Important Feature Set: MAE – 4.39, MSE – 42.65, R2 – 0.47
Even though we are using only 6 six features, our optimized models are producing the errors which are only slightly more than the case where models were built using the full feature set. Whether to go for the optimized model or not is really a choice of how much error can you bear in your predictions.
Ridge Regression
Perform the hyperparameter tuning for the Ridge regression, and fit the ridge regression model on the important feature data set with the best parameters in the context of ‘neg_mean_absolute_error’:
ridge_model = Ridge()
ridge_param_grid = {'solver': ['svd', 'cholesky', 'lsqr', 'sag'],
'alpha': [1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 1, 10, 100],
'fit_intercept': [True, False],
'normalize': [True, False]
}
ridge_cv = KFold(n_splits=5)
ridge_grid = GridSearchCV(ridge_model, ridge_param_grid, cv=ridge_cv, scoring='neg_mean_absolute_error', n_jobs=-1)
ridge_grid.fit(X_train_imp, y_train_imp)
print('Ridge Regression Best Params:', ridge_grid.best_params_)
print('Ridge Regressiton Best Score:', ridge_grid.best_score_)
Output:
Ridge Regression Best Params: {'alpha': 0.001, 'fit_intercept': False, 'normalize': True, 'solver': 'lsqr'}
Ridge Regression Best Score: -3.4295209884643554
Now predict the house prices of the test data set and evaluate the performance of the optimized Ridge regression model:
ridge_y_pred = ridge_grid.predict(X_test_imp)
print('Mean Absolute Error:', mean_absolute_error(y_test_imp, ridge_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test_imp, ridge_y_pred))
print('R2 Score:', r2_score(y_test_imp, ridge_y_pred))
Output:
Mean Absolute Error: 4.0980783
Mean Squared Error: 41.441013
R2 Score: 0.4910744142511475
Full Feature Set: MAE – 3.91, MSE – 36.11, R2 – 0.55
Important Feature Set: MAE – 4.09, MSE – 41.44, R2 – 0.49
Regression Modelling using Support Vector Machine
To train the SVM model on the Housing data set, Support Vector Regressor (SVR) is employed from scikit-learn library.
Full Feature Set
At first, SVR() model is fitted on the training data having full features using the default parameters:
svm_model = SVR()
svm_model.fit(X_train, y_train)
Once the model is trained, we need to predict the performance of the model on the testing data set:
svm_y_pred = svm_model.predict(X_test)
print('Mean Absolute Error:', mean_absolute_error(y_test, svm_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test, svm_y_pred))
print('R2 Score:', r2_score(y_test, svm_y_pred))
Output:
Mean Absolute Error: 3.611750709767946
Mean Squared Error: 41.06053610851429
R2 Score: 0.49574697163034387
We have got a comparable model to Linear/Ridge Regression, but SVM is much more complicated than both of those. It seems like the selection of default parameters is costing us the desired accuracy of the regression model
Let’s now tune hyper-parameters for SVM and evaluate whether we can further enhance the performance of the SVM regression model.
In this alternative approach, we will train the model using a subset of hyperparameters and then select best parameters based on a scoring metric i.e., neg_mean_absolute_error:
svm_param_grid = {'C':[0.01, 0.1, 1, 10, 100],
'kernel': ['linear', 'rbf'],
'gamma' :[0.01, 0.1, 1, 10, 100]}
svm_cv = KFold(n_splits=5)
svm_grid = GridSearchCV(SVR(), svm_param_grid, cv=svm_cv, scoring='neg_mean_absolute_error', n_jobs=-1)
svm_grid.fit(X_train, y_train)
‘C’ is the regularization parameter which controls the amount of error in the training data as well as the unseen data. Higher value of ‘C’ leads to less regularization which results in overfitting for training data and vice versa.
‘Kernel’ is selected based on the shape/dimension of the input features.
‘gamma’ decides how much curvature we want in a decision boundary. Higher ‘gamma’ leads to more curvature which results in overfitting and vice versa
SVR() model will be trained using each combination of the hyperparameters specified in ‘svm_param_grid’.
During each iteration, model will be trained using 5-fold cross-validation. 4-folds of the data will be used to train the model, and remaining fold will be used to test the accuracy of the trained model.
Hyperparameters resulting in the maximum accuracy will be used to train the model on the complete dataset in the final stages of ‘GridSearchCV’. We can get the parameters which resulted in the maximum accuracy as follows:
print('SVM Best Params:', svm_grid.best_params_)
print('SVM Best Score:', svm_grid.best_score_)
Output:
SVM Best Params: {'C': 100, 'gamma': 0.1, 'kernel': 'rbf'}
SVM Best Score: -2.161312587590899
Let’s evaluate the performance of the tuned SVM model on the test dataset:
svm_y_pred = svm_grid.predict(X_test)
print('Mean Absolute Error:', mean_absolute_error(y_test, svm_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test, svm_y_pred))
print('R2 Score:', r2_score(y_test, svm_y_pred))
Output:
Mean Absolute Error: 2.7499940881714577
Mean Squared Error: 20.401810859231365
R2 Score: 0.7494510329138371
So, we have significantly improved our accuracy with the optimized hyperparameters for the support vector regressor.
Important Feature Set
Let’s now train SVR() model on the data set containing important features using the default parameters:
svm_model = SVR()
svm_model.fit(X_train_imp, y_train_imp)
svm_y_pred = svm_model.predict(X_test_imp)
print('Mean Absolute Error:', mean_absolute_error(y_test_imp, svm_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test_imp, svm_y_pred))
print('R2 Score:', r2_score(y_test_imp, svm_y_pred))
Output:
Mean Absolute Error: 5.50653027623757
Mean Squared Error: 80.77879198713099
R2 Score: 0.007978113585639601
Oops… Not acceptable for me at all!
Its time that we tune the hyperparameters for the important feature set as well:
svm_param_grid = {'C':[0.01, 0.1, 1, 10],
'kernel': ['linear', 'rbf'],
'gamma' :[0.01, 0.1, 1, 10]}
svm_cv = KFold(n_splits=5)
svm_grid = GridSearchCV(SVR(), svm_param_grid, cv=svm_cv, scoring='neg_mean_absolute_error', n_jobs=-1)
svm_grid.fit(X_train_imp, y_train_imp)
print('SVM Best Params:', svm_grid.best_params_)
print('SVM Best Score:', svm_grid.best_score_)
Output:
SVM Best Params: {'C': 10, 'gamma': 0.01, 'kernel': 'rbf'}
SVM Best Score: -3.113660588140698
svm_y_pred = svm_grid.predict(X_test_imp)
print('Mean Absolute Error:', mean_absolute_error(y_test_imp, svm_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test_imp, svm_y_pred))
print('R2 Score:', r2_score(y_test_imp, svm_y_pred))
Output:
Mean Absolute Error: 3.6375910893171888
Mean Squared Error: 35.190144854497014
R2 Score: 0.5678396145449389
SVM regression model has shown an overall improved performance on the important feature set when compared to Linear/Ridge regression.
If you look closely, performance of Linear/Ridge regression on the full feature set is comparable to SVM model on the important feature set.
Seems like we are getting there, right?
Let’s now train Random Forest Classifier model on the same data set…
Regression Modelling using Random Forest Regressor
In Random Forest Regressor, a lot of decision tree regressors with sparse feature set and nodes/leaves are trained using the training data set. During the prediction stage, each decision tree in the Random Forest model predicts an output value. The mean of all these values then reported as the final predicted value for each instance in the test data set.
Full Feature Set
Let’s first train the Random Forest Regressor model using the full feature training data:
rf_model = RandomForestRegressor()
rf_model.fit(X_train, y_train)
Let’s observe the accuracy of the Random Forest model on the test data set:
rf_y_pred = rf_model.predict(X_test)
print('Mean Absolute Error:', mean_absolute_error(y_test, rf_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test, rf_y_pred))
print('R2 Score:', r2_score(y_test, rf_y_pred))
Output:
Mean Absolute Error: 2.6680392169017417
Mean Squared Error: 19.543470825446068
R2 Score: 0.7599920682345473
Nice… This is the best trained model so far. Let’s see how Random Forest behaves in front of reduced feature set.
Important Feature Set
rf_model = RandomForestRegressor()
rf_model.fit(X_train_imp, y_train_imp)
rf_y_pred = rf_model.predict(X_test_imp)
print('Mean Absolute Error:', mean_absolute_error(y_test_imp, rf_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test_imp, rf_y_pred))
print('R2 Score:', r2_score(y_test_imp, rf_y_pred))
Output:
Mean Absolute Error: 2.959068677846123
Mean Squared Error: 25.99959658641793
R2 Score: 0.6807061826849344
Full Feature Set: MAE – 2.66, MSE – 19.54, R2 – 0.76
Important Feature Set: MAE – 2.95, MSE – 25.99, R2 – 0.68
With these results, the magic of important features seems to be working. The only question is whether you can select the right model for your application.
Let’s see if we can extract more improved results with Gradient Boosting Regressor…
Regression Modelling using Gradient Boosting Regressor
Gradient Boosting classifier is a combined sequential model of various Decision Trees, where the outcome of one decision tree is used to train the next one and so on.
Let’s train and evaluate the performance of gradient boosting regressor on both the full feature set and the important feature set…
Full Feature Set
gb_model = GradientBoostingRegressor()
gb_model.fit(X_train, y_train)
gb_y_pred = gb_model.predict(X_test)
print('Mean Absolute Error:', mean_absolute_error(y_test, gb_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test, gb_y_pred))
print('R2 Score:', r2_score(y_test, gb_y_pred))
Output:
Mean Absolute Error: 2.6457781465159815
Mean Squared Error: 16.877334306288596
R2 Score: 0.7927341495916711
So now you see… Our mean squared error for Gradient boosting regressor is almost half than that of Linear/Ridge regression model.
Moreover, gradient boosting regressor seems to produce the least MAE, MSE, and R2 score amongst all the algorithms trained for the Boston housing dataset.
Let’s see if the similar trend is observed for the important features of the dataset…
Important Feature Set
gb_model = GradientBoostingRegressor()
gb_model.fit(X_train_imp, y_train_imp)
gb_y_pred = gb_model.predict(X_test_imp)
print('Mean Absolute Error:', mean_absolute_error(y_test_imp, gb_y_pred))
print('Mean Squared Error:', mean_squared_error(y_test_imp, gb_y_pred))
print('R2 Score:', r2_score(y_test_imp, gb_y_pred))
Output:
Mean Absolute Error: 2.912611985891981
Mean Squared Error: 23.34475952053617
R2 Score: 0.7133094985978334
Full Feature Set: MAE – 2.64, MSE – 16.87, R2 – 0.79
Important Feature Set: MAE – 2.91, MSE – 23.34, R2 – 0.71
Gradient Boosting regressor also seems to produce the best training model amongst all the tried algorithms even when half the features are stripped off. Nice, isn’t it?
Conclusion
In this tutorial, we developed regression models to predict the house prices in suburbs of Boston using Linear/Ridge Regression, Support Vector Regressor, Random Forest Regressor and Gradient Boosting Regressor. These regression models helped us estimate the house prices using the numeric input features. Moreover, the models were also trained using the more correlated features of the data set, and their performance was compared with the models developed using the full-fledge feature set.
Gradient Boosting Regressor and Random Forest Regressor were more robust in predicting the house prices even when provided with a limited feature set. These results depicted that robust model could be trained using the important features only, which is a critical requirement to save computation resources as well as the training time.

He is the owner and founder of Embedded Robotics and a health based start-up called Nema Loss. He is very enthusiastic and passionate about Business Development, Fitness, and Technology. Read more about his struggles, and how he went from being called a Weak Electrical Engineer to founder of Embedded Robotics.

Subscribe for Latest Articles
Don't miss new updates on your email!