In this tutorial, you will learn how to use TensorFlow and Keras API for image classification using CNN (Convolutional Neural Network).
We will train multi-class CNN models using MNIST and CIFAR10 datasets, both of which contain 10 classes and can be loaded directly using Keras. Finally, we will evaluate the validation accuracy of the trained CNN models using the test data set.
This tutorial will feature following tools/libraries to classify images:
- Python
- Jupyter Notebook
- TensorFlow
- Keras
- pandas
- matplotlib
Article Contents
Article Notebook
Code: Image Classification using CNN via TensorFlow and Keras
Prepared By: Awais Naeem (awais.naeem@embedded-robotics.com)
Copyrights: www.embedded-robotics.com
Disclaimer: This code can be distributed with the proper mention of the owner copyrights
Notebook Link: https://github.com/embedded-robotics/datascience/blob/master/mnist_dataset_image_multiclass_cnn/cnn_mnist_cifar10.ipynb
MNIST Dataset Image Classification using CNN
MNIST dataset contains grayscale images of handwritten digits from 0-9. There are a total of 60,000 examples in the training dataset and 10,000 examples in the test data set. The digits have been size-normalized and centered in a fixed-size image of 28×28 pixels.
Dataset Link: http://yann.lecun.com/exdb/mnist/
Input Data: Two-dimensional array having size (28,28) depicting the pixel values in an image
Output Labels: Discrete values between 0-9 (inclusive) corresponding to the handwritten digit
Data Reading and Pre-Processing
Let’s first import all python-based libraries necessary to read the data and process it using Tensforflow and Keras API:
import os
import numpy as np
import pandas as pd
import ssl
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense, Conv2D, MaxPool2D, Flatten, Dropout
from tensorflow.keras.datasets import mnist, cifar10
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
Download the MNIST data directly using Keras, and load into train/test datasets:
(X_train, y_train), (X_test, y_test) = mnist.load_data()
Firstly, verify the shape of the data to cater to any ambiguities:
print('X_train Shape: ', X_train.shape)
print('y_train Shape: ', y_train.shape)
print('X_test Shape: ', X_test.shape)
print('y_test Shape: ', y_test.shape)
Output:
X_train Shape: (60000, 28, 28)
y_train Shape: (60000,)
X_test Shape: (10000, 28, 28)
y_test Shape: (10000,)
So, input training data contains 60000 images with each image having a dimension of (28 x 28) whereas output training data contains the class labels for the images.
To visualize the images, we can plot the first 100 occurrences from the training data set using matplotlib:
plt.figure(figsize=(15,10))
for i in range(100):
plt.subplot(10,10,i+1)
plt.imshow(X_train[i], cmap=plt.get_cmap('gray'))
plt.subplots_adjust(wspace=None, hspace=None)
plt.show()
Since each image is grayscale and has dimensions of (28,28), we need to add the channel information to image shape, else convolution neural network won’t make sense of the input images at all.
For a grayscale image, each image should have a shape of (28,28,1) because grayscale image uses only 1 channel rather than the colored images which use 3 channels.
X_train = X_train.reshape((X_train.shape[0], X_train.shape[1], X_train.shape[2], 1))
X_test = X_test.reshape((X_test.shape[0], X_test.shape[1], X_test.shape[2], 1))
print(X_train.shape)
print(X_test.shape)
Output:
(60000, 28, 28, 1)
(10000, 28, 28, 1)
To make the pixel values consistent across all the images, we need to normalize the training and test data. This will also ensure that neural networks do not optimize on large weight values during the training phase:
X_train = X_train.astype('float32')/255.0
X_test = X_test.astype('float32')/255.0
Image normalization by using 255 as a divisor is pretty much standard everywhere because pixels values range from 0-255 whether it’s a grayscale image or a colored one.
Before we go on to make the architecture for neural network, it’s better to record the image shape and unique number of class labels:
image_shape = X_train.shape[1:]
n_classes = len(np.unique(y_train))
Training the CNN Model
Let’s now build the architecture for neural network to classify the handwritten digits. Neural network consists of multiple layers, each one taking input from the previous one and advancing output to the next one. The first layer takes the image as input, and the last layer gives the prediction label as the output.
We can define a sequential () model to embed the layers of CNN. Later, we can add as many layers as we want in this sequential model:
model = Sequential()
First layer will take image as the input and extract the relevant features to be used for training purposes. These features are extracted using the convolution layer by specifying number of filters, kernel size and activation function.
model.add(Conv2D(filters=32, kernel_size=(3,3), padding="same", activation="relu", kernel_initializer="he_uniform", input_shape=image_shape))
Each filter can be used to extract a distinct feature from the image e.g., edges, sharpness, orientation, rotation, eyes, nose, ears, etc. Kernel size determines how much portion of the image will be convolved with the kernel in a single go.
Once the features are calculated, these are passed through non-linear activation function ‘relu’ i.e., f(x) = max (0, x). Such an activation makes the features non-linear to align with the non-linear nature of the images.
Same amount of padding is necessary if you want to keep the dimensions same between the input and the output of the convolution layer.
Once the convolution is done for all the filters, we need to pool the output features to reduce the noisy features. This can be done using a pooling layer which performs a dedicated operation on the sparse set of features to come up with a single feature.
For this tutorial we will use a max pooling layer which will select the feature having the maximum value from the selected feature pool:
model.add(MaxPool2D(pool_size=(2,2)))
The pool size of (2,2) depicts that pooling operation will be performed on 4 features adjacent to each other in a rectangle shape. After the pooling operation is done, a stride of 2 will be taken in horizontal/vertical position. This operation will reduce the number of features to half for each filter.
We can repeat this combination of convolution and pooling layers to get more features about the data. But we will only go with a single combination for MNIST data, because a handwritten digit is only a simple combination of grayscale pixels.
Now we need to add a flatten layer to convert the 2-dimensional features into a single dimension so that we can feed these features into a fully connected layer for further training/prediction purposes.
model.add(Flatten())
model.add(Dense(units=100, activation='relu', kernel_initializer='he_uniform'))
Here, Dense() layer is a fully connected layer with 100 units and ‘relu’ activation function. To avoid overfitting with the training data, we can drop a certain set of neurons (20%) using the Dropout() layer:
model.add(Dropout(0.2))
Now, we need to add a final layer having the same no. of units as the output classes and the activation function equivalent to ‘softmax’. This activation gives the probability of the input image for each of the output layer units. The unit having the maximum probability is then classified as the output label:
model.add(Dense(units = n_classes, activation='softmax'))
We can see the model architecture as follows:
model.summary()
Output:
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 28, 28, 32) 320
max_pooling2d (MaxPooling2D (None, 14, 14, 32) 0
)
flatten (Flatten) (None, 6272) 0
dense (Dense) (None, 100) 627300
dropout (Dropout) (None, 100) 0
dense_1 (Dense) (None, 10) 1010
=================================================================
Total params: 628,630
Trainable params: 628,630
Non-trainable params: 0
Now, we need to compile the model and specify the optimizer, loss and accuracy parameters:
model.compile(optimizer='adam', loss = 'sparse_categorical_crossentropy', metrics=['accuracy'])
Since our dataset is multi-class, we will specify the loss to be ‘sparse categorical crossentropy’. The loss value is the parameter which the ‘adam’ optimizer will minimize by tweaking the weights during the training phase.
Essentially, ‘adam’ optimizer tries to find the global minima for the loss value among all the local minima by optimizing the trainable parameters. Moreover, ‘accuracy’ of the model will be reported for each training batch/epoch to gauge the convergence of the neural network.
Before the training, we need to specify the number of epochs for which the network need to be trained. Obviously, we are not sure about the magic number and we tend to take an educated guess.
Let’s just say that we specified the number of epochs to be 100 whereas our model was converged to minimum validation loss after 10 epochs. The remaining 90 epochs will only tend to overfit the model on the training data. So, how will we avoid this situation?
It’s simple… You specify the callback for EarlyStopping(), which will halt the model training after the model fails to minimize the validation loss value after the stated no. of epochs in the callback parameters.
checkpoint_filepath = os.getcwd()
model_checkpoint_callback = ModelCheckpoint(filepath=checkpoint_filepath, save_weights_only=False, monitor='loss', mode='min', save_best_only=True)
callbacks = [EarlyStopping(patience=2), model_checkpoint_callback]
Along with the callback for EarlyStopping(), you can specify the ModelCheckpoint() to monitor the loss after each epoch and save the best model.
Now, we are at the stage where we need to start training the model by specifying the training data, batch size and number of epochs. Since we have specified the callback to monitor the loss on the validation dataset, we need to specify the validation data as well.
history = model.fit(X_train, y_train, batch_size=128, epochs=10, validation_data = (X_test, y_test), callbacks=callbacks)
Neural network takes in the input images in specific batches rather than taking all of them at once. This technique does not fill all the RAM at once, and also helps in distributed computing.
A single epoch specifies the training done on the whole set of input images. This neural network will get trained on 10 epochs, in which the latest epoch will use the weight tuned in the last epoch. If the validation loss of the model is not minimized for two consecutive number of epochs, the training of the model will halt as specified in the callback.
After the model training, it was observed that the model training was halted after 7 epochs because the validation loss did not improve after 5 epochs.
Since we saved the model params in the ‘history’ variable, we can visualize the training/testing data loss and accuracy:
metrics_df = pd.DataFrame(history.history)
print(metrics_df)
Output:
loss accuracy val_loss val_accuracy
0 0.144980 0.957900 0.064440 0.9803
1 0.099907 0.970917 0.052243 0.9829
2 0.082729 0.975933 0.046908 0.9840
3 0.068244 0.979467 0.041944 0.9865
4 0.061921 0.980700 0.042802 0.9859
5 0.055164 0.982850 0.043078 0.9858
6 0.048413 0.984933 0.043730 0.9862
We can also visualize the loss and accuracy for training/testing data over the number of epochs using matplotlib:
plt.figure(figsize=(10,5))
plt.plot(metrics_df.index, metrics_df.loss)
plt.plot(metrics_df.index, metrics_df.val_loss)
plt.title('MNIST Model Loss over Epochs')
plt.xlabel('Epochs')
plt.ylabel('Categorical Crossentropy')
plt.legend(['Training Loss', 'Validation Loss'])
plt.show()
plt.figure(figsize=(10,5))
plt.plot(metrics_df.index, metrics_df.accuracy)
plt.plot(metrics_df.index, metrics_df.val_accuracy)
plt.title('MNIST Model Accuracy over Epochs')
plt.xlabel('Epochs')
plt.ylabel('Acuracy')
plt.legend(['Training Accuracy', 'Validation Accuracy'])
plt.show()
So, we get a whopping 98.5% accuracy on the MNIST data set by training a simple neural network. Let’s see what we can get out of the CIFAR10 dataset.
CIFAR10 Dataset Image Classification using CNN
The CIFAR-10 dataset consists of 60000 colored images having size (32 x 32) and divided into ten classes with 6000 images per class. Dataset classes include Airplane, Automobile, Bird, Cat, Deer, Dog, Frog, Horse, Ship, and Truck. There are a total of 50,000 training images and 10,000 test images.
Dataset Link: https://www.cs.toronto.edu/~kriz/cifar.html
Input Data: Three-dimensional array having size (32,32,3) depicting the pixel values in each channel of the colored image i.e., red, blue, and green
Output Labels: Discrete values between 0-9 (inclusive) corresponding to the image class as follows:
0 – Airplance
1 – Automobile
2 – Bird
3 – Cat
4 – Deer
5 – Dog
6 – Frog
7 – Horse
8 – Ship
9 – Truck
Data Reading and Pre-Processing
Firstly, load the CIFAR10 data set and divide into training/testing sets. You may also want to skip the certificate verification if you do not have a valid certificate:
ssl._create_default_https_context = ssl._create_unverified_context
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
print('X_train Shape: ', X_train.shape)
print('y_train Shape: ', y_train.shape)
print('X_test Shape: ', X_test.shape)
print('y_test Shape: ', y_test.shape)
Output:
X_train Shape: (50000, 32, 32, 3)
y_train Shape: (50000, 1)
X_test Shape: (10000, 32, 32, 3)
y_test Shape: (10000, 1)
From the data shape, it looks like the images are colored with 3-channels and dimensions (32 x 32). Let’s visualize first 50 images in the dataset:
plt.figure(figsize=(15,10))
for i in range(50):
plt.subplot(5,10,i+1)
plt.imshow(X_train[i])
plt.show()
Next step is to normalize the image pixels so that neural network gets converged on low values of training weights:
X_train = X_train.astype('float32')/255.0
X_test = X_test.astype('float32')/255.0
Training the CNN Model
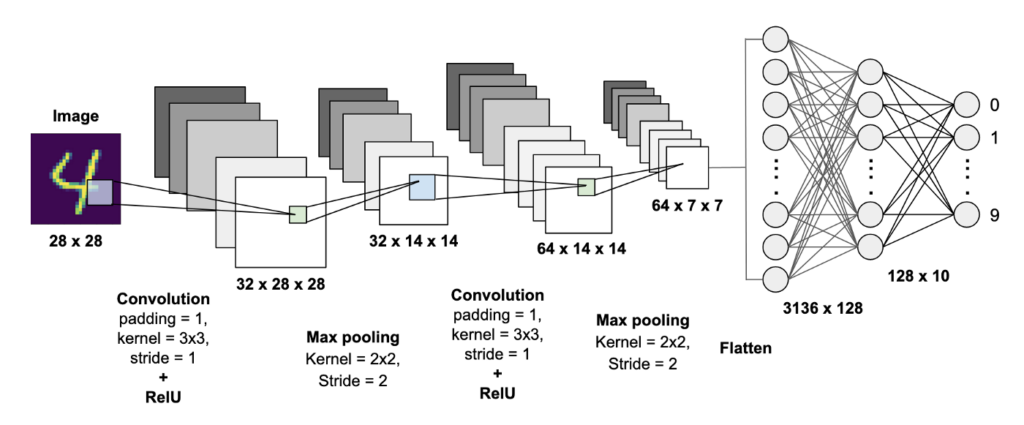
Now, we need to create the neural network architecture. This time, we will create two convolution layers; the first one with 32 filters and the next one with 64 filters, whereas kernel size will remain the same in both of the layers. A max-pooling layer will come after each convolution layer to select only the significant features.
After the Flatten() layer, a fully connected layer with 100 units will be added followed by a dropout layer to randomly 20% of the neurons. The last layer will have 10 units with the ‘softmax’ activation because there are 10 output classes in the dataset:
model = Sequential()
model.add(Conv2D(filters=32, kernel_size=(3,3), padding="same", activation="relu", input_shape = image_shape))
model.add(MaxPool2D(pool_size=(2,2), strides=2))
model.add(Conv2D(filters=64, kernel_size=(3,3), padding="same", activation="relu"))
model.add(MaxPool2D(pool_size=(2,2), strides=2))
model.add(Flatten())
model.add(Dense(units=100, activation="relu"))
model.add(Dropout(0.2))
model.add(Dense(units=10, activation="softmax"))
Let’s visualize the model summary:
model.summary()
Output:
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 32, 32, 32) 896
max_pooling2d_1 (MaxPooling (None, 16, 16, 32) 0
2D)
conv2d_2 (Conv2D) (None, 16, 16, 64) 18496
max_pooling2d_2 (MaxPooling (None, 8, 8, 64) 0
2D)
flatten_1 (Flatten) (None, 4096) 0
dense_2 (Dense) (None, 100) 409700
dropout_1 (Dropout) (None, 100) 0
dense_3 (Dense) (None, 10) 1010
=================================================================
Total params: 430,102
Trainable params: 430,102
Non-trainable params: 0
Compile the model, and specify the callbacks with the EarlyStopping() value to be 5 epochs:
model.compile(optimizer="adam", loss="sparse_categorical_crossentropy", metrics=['accuracy'])
checkpoint_filepath = os.getcwd()
model_checkpoint_callback = ModelCheckpoint(filepath=checkpoint_filepath, save_weights_only=False, monitor='loss', mode='min', save_best_only=True)
callbacks = [EarlyStopping(patience=5), model_checkpoint_callback]
Now fit the model with 100 epochs and the default batch size of 32:
history = model.fit(X_train, y_train, epochs=100, validation_data=(X_test, y_test), callbacks=callbacks)
The optimizer function gets converged after 8 epochs, after which the validation loss value tends to increase. We can now create a panda DataFrame for the loss and accuracy values for all the epochs:
metrics_df = pd.DataFrame(history.history)
print(metrics_df)
Output:
loss accuracy val_loss val_accuracy
0 1.473789 0.46542 1.192456 0.5854
1 1.132276 0.59744 1.021795 0.6412
2 1.003781 0.64640 0.922838 0.6807
3 0.918577 0.67578 0.899950 0.6881
4 0.845265 0.70214 0.870915 0.6968
5 0.777231 0.72302 0.905810 0.6851
6 0.730103 0.73994 0.876937 0.7071
7 0.677579 0.75824 0.883064 0.7043
8 0.635262 0.77246 0.870179 0.7102
9 0.599407 0.78600 0.866151 0.7147
10 0.559124 0.79908 0.875302 0.7153
11 0.526724 0.80936 0.922980 0.7080
12 0.489864 0.82106 0.960135 0.7088
13 0.462804 0.82994 1.028358 0.6962
14 0.440208 0.83730 1.012244 0.7135
Now we can plot the accuracy and loss for both the training and testing datasets as a function of the training epochs:
plt.figure(figsize=(10,5))
plt.plot(metrics_df.index, metrics_df.loss)
plt.plot(metrics_df.index, metrics_df.val_loss)
plt.title('CIFAR10 Model Loss over Epochs')
plt.xlabel('Epochs')
plt.ylabel('Categorical Crossentropy')
plt.legend(['Training Loss', 'Validation Loss'])
plt.show()
plt.figure(figsize=(10,5))
plt.plot(metrics_df.index, metrics_df.accuracy)
plt.plot(metrics_df.index, metrics_df.val_accuracy)
plt.title('MNIST Model Accuracy over Epochs')
plt.xlabel('Epochs')
plt.ylabel('Acuracy')
plt.legend(['Training Accuracy', 'Validation Accuracy'])
plt.show()
Conclusion
In this tutorial, we trained CNN models for multiclass MNIST and CIFAR10 datasets using TensorFlow and Keras API. Both the datasets were loaded directly from the Keras API into training/test datasets. A custom neural network architecture was built for each of the dataset, and then trained using the training dataset. A call back was used to halt the model training if the validation loss was not minimized for two consecutive epochs during the training phase.
For the MNIST dataset, the model was able to classify the test images with almost 98.5% accuracy. Whereas the test images of CIFAR10 dataset were classified with an accuracy of around 72%. These accuracy values can further be improved by using a different neural network architecture and/or data pre-processing and parameters augmentation.
He is the owner and founder of Embedded Robotics and a health based start-up called Nema Loss. He is very enthusiastic and passionate about Business Development, Fitness, and Technology. Read more about his struggles, and how he went from being called a Weak Electrical Engineer to founder of Embedded Robotics.
Subscribe for Latest Articles
Don't miss new updates on your email!